推荐阅读：2021陕西公务员行测每日一练(1月6日)【点击查看】
解析
1.第一步，本题考查行程问题，属于相遇追及类，用公式法解题。
第二步，第一次相遇时甲走了80分钟，第二次相遇时甲走了80+20=100(分钟)，乙从第一次与甲相遇到第二次与甲相遇期间，共走20分钟，走了甲80分钟+甲100分钟的路程，所以乙走20分钟的路程相当于甲走180分钟的路程，即甲乙速度之比为1∶9(路程一定，速度和时间成反比)，赋值甲的速度是1，那么乙的速度为9，AB两地距离为S=(1+9)×80=800，那么甲到达B地用时800分钟。
第三步，根据两端出发多次相遇问题公式，设甲乙相遇n次，则(2n-1)×800=(1+9)×800，解得x=5.5，即相遇了5次。
因此，选择A选项。
2.第一步，本题考查基础应用题，用方程法解题。
第二步，设原来第一个、第二个、第三个书架上的书分别为x、y、z，三次移动后三个书架书籍情况如下：
第三步，根据三个书架最终册数完全相同，则有2(x-y)=2y-z①，2y-z=2z-(x-y)②。消去y可得，可得4(3z-x)=2x+z，所以11z=6x，所以x∶z=11∶6。
因此，选择D选项。
3.第一步，数列变化趋势较快，尝试倍数递推，递推积无明显规律，考虑平方递推数列。
第二步，观察数列发现4=[1+(-3)]²，1=(-3+4)²，25=(4+1)²，规律为第三项=(第一项+第二项)²，所求项为(1+25)²=676(也可用尾数法，尾数为6)。
因此，选择D选项。
4.第一步，数列变化趋势平缓，优先考虑做差。
第二步，做差如图所示：
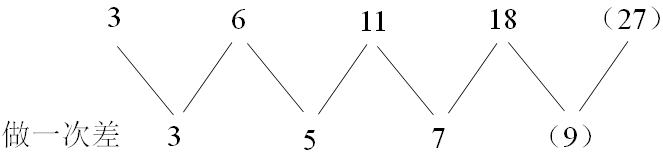
差数列是公差为2的等差数列，下一项为7+2=9，则所求项为18+9=27。
因此，选择A选项。
5.解法一：第一步，数列正负交替变化，考虑做和。
第二步，做和如图所示：
和数列为1，-2，3，-4，则下一项为5，所求项为5-(-12)=17。
因此，选择B选项。
解法二：考虑做差。数列正负交替，奇数项为负，偶数项为正，所求项为偶数项，则所求项为正数，对数列取绝对值，发现新数列变化趋势平缓，考虑做差，做差如图所示：
差数列是公差为1的等差数列，下一项为4+1=5，则所求项为12+5=17。
因此，选择B选项。
6.第一步，本题考查排列组合问题，属于基础排列组合。
第二步，根据“倒数第一位是奇数”，可知倒数第一位有5种情况;再考虑倒数第二位，有10种情况。故最后两位数字可能的组合有5×10=50(种)，即最多拨号50次才能保证拨对朋友的手机号码。
因此，选择B选项。
7.第一步，本题考查基础应用题，使用十字交叉法解题。
第二步，十字交叉如下：
可知股票与基金之比为3%∶15%=1∶5。
因此，选择B选项。
8.解法一：
第一步，本题考查基础计算问题。
第二步，原式=33333×(3×22222+33334)=33333×100000=3333300000。
因此，选择B选项。
解法二：
第一步，本题考查基础计算问题，用数字特性法解题。
第二步，由于99999和33333均为3的倍数，故答案也必是3的倍数，只有B选项符合。
因此，选择B选项。
9.第一步，本题考查基础行程问题，用公式法解题。
第二步，小林的速度为x公里/小时，则老林的速度为(x+6)公里/小时，10分钟=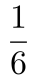
小时，老林追上小林时距离工厂500米，可知两人均走了1.5-0.5=1(公里)，但小林比老林多用
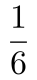小时，根据行程问题基础公式：t=
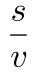，可列方程：
-
=。
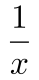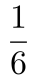因此，选择A选项。
10.解法一：
第一步，本题考查工程问题，属于条件类，用方程法解题。
第二步，设原效率为每小时植树x棵，则实际效率为1.2x。提前20分钟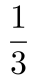
小时完成任务，可得
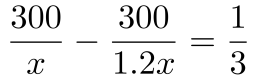，解得x=150。
因此，选择B选项。
解法二：
第一步，本题考查工程问题，属于条件类，用比例法解题。
第二步，实际效率为原来的1.2倍，可得效率前后比为5∶6，则时间前后比为6∶5。由提前20分钟完成任务，可得原来工作时间为20×6=120(分钟)，即2小时。故原来每小时植树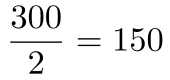
(棵)。
因此，选择B选项。
图图推荐：
省考公告预约：http://sn.huatu.com/zt/2021skggyy/
上岸直通车：http://sn.huatu.com/zt/2021sksaztc/
